Rumus Untuk Menentukan Sampling Dengan Beberapa Referensi Para Ahli
Beberapa pendapat ahli mengenai ukuran sampel penelitian
* Berasal dari luar Indonesia
1. Ukuran sampel dengan teori slovin (1960)
Salah satu literatur yang paling banyak digunakan adalah penentuan ukuran sampel menggunakan rumus slovin (1960). Seorang ahli yang bernama slovin ini ternyata sampai saat ini belum diketahui Siapa nama aslinya, bahkan pernah menjadi perdebatan mengenai tahun terbit dari naskah yang ditulis oleh slovin ini yaitu tahun 1960 dan 1843. Dalam tulisan Riduwan (2005), dengan judul penelitian “belajar mudah penelitian untuk guru”, dia mengutip rumus slovin dengan formula sebagai berikut;
RUMUS SAMPEL : RUMUS SLOVIN
[alert-note] n=N1+Ne2 [/alert-note]
n= besar sampel yang ;
N= ukuran populasi atau jumlah elemen dalam populasi ;
e= nilai presisi atau tingkat signifikansi yang telah ditentukan. Umumnya dalam penelitian tingkat signifikansi ditentukan sebesar 95% atau 0,05.
CONTOH PENENTUAN UKURAN SAMPEL DENGAN RUMUS SLOVIN
Misalkan satu populasi berukuran Rp1.000 elemen/anggota, akan dilakukan survei dengan mengambil beberapa sampel menggunakan rumus slovin. Mata perhitungan sederhana dalam menentukan jumlah sampel adalah sebagai berikut;
Diketahui;
N= 1,000 orang
e= dengan tingkat signifikansi sebesar 95% atau 0,05
Maka;
n ≈ 286
Karena sampel kita harus berupa angka bulat dan orang, maka kita lakukan pembulatan mengikuti aturan pembulatan standar yaitu, apabila ≥ 0,5 maka kita bulatkan ke atas dan sebaliknya.
2. Menentukan ukuran sampel dengan formula Cochran, W. G. (1977)
Cochran, W. G. (1977), dalam bukunya berjudul “Sampling techniques” edisi ke 3 menjelaskan suatu formula sampling yang dapat anda jadikan referensi. Cochran membagi 2 teknik menentukan sampel berdasarkan data populasi yang bersifat kontinu dan bersifat kategori.
FORMULA COCHRAN UNTUK DATA KATEGORI
[alert-note]n=z2(p)(q)e2 [/alert-note]
dimana:
n = ukuran sampel yang akan kita cari
z = nilai tabel z ( tabel distribusi normal) pada tingkat kepercayaan tertentu. Lihat tabel z disini
p = proporsi kategori dari total seluruh kategori. Nilainya berupa nilai desimal antara 0-1, misal 0.5, 0.2, dst.
q = proporsi kategori lain selain p yang juga dituliskan sebagai (1-p)
e = margin error
Contoh :
Sebagai contoh, katakan kita ingin mengevaluasi program penyuluhan yang mengajak petani untuk menggunakan metode baru. Anggaplah populasinya besar tetapi kita tidak tahu persentase dari penerimaan metode baru tersebut. Oleh karena itu, kita berasumsi tingkat penerimaannya 50:50 atau p = 0,5. Selanjutnya kita pilih α = 0,05 dan keakuratan 5% . Jumlah sampel yang diperlukan adalah sebagai berikut:
*(sumber contoh bisa dilihat di: hattastat)
FORMULA COCHRAN UNTUK DATA KONTINYU
[alert-note]n=z2s2e2 [/alert-note] dimana,
n = ukuran sampel yang akan dicari
z = nilai z berdasarkan pada alpha tertentu, lihat tabel z
s = standard deviasi dari populasi, dan
e = margin error
n = ukuran sampel yang akan dicari
z = nilai z berdasarkan pada alpha tertentu, lihat tabel z
s = standard deviasi dari populasi, dan
e = margin error
* Berasal dari indonesia
3. Menentukan ukuran sampel dengan Menurut Supranto J (2000)
Menurut Supranto J (2000) untuk penelitian eksperimen dengan rancangan acak lengkap, acak kelompok atau faktorial, secara sederhana dapat dirumuskan:
(t-1) (r-1) > 15
dimana : t = banyaknya kelompok perlakuan
j = jumlah replikasi
Contoh kasus Rumus Besar Sampel Penelitian Eksperimen
Contohnya: Jika jumlah perlakuan ada 4 buah, maka jumlah ulangan untuk tiap perlakuan dapat dihitung:
(4 -1) (r-1) > 15
(r-1) > 15/3
r > 6
Untuk mengantisipasi hilangnya unit ekskperimen maka dilakukan koreksi dengan 1/(1-f) di mana f adalah proporsi unit eksperimen yang hilang atau mengundur diri atau drop out.
4. Penelitian ukuran sampel dengan Menurut Suyatno (2001)
Dari hasil hasil penelitian Suyatno (2001) di daerah Demak-Jawa Tengah, proporsi bayi (p) yang diberi makanan ASI eksklusif sekitar 17,2 %. Ini berarti nilai p = 0,172 dan nilai q = 1 – p. Dengan limit dari error (d) ditetapkan 0,05 dan nilai Alfa = 0,05, maka jumlah sampel yang dibutuhkan sebesar:
= 219 orang (angka minimal)
Jika tidak diketemukan nilai p dari penelitian atau literatur lain, maka dapat dilakukan maximal estimation dengan p = 0,5. Jika ingin teliti teliti maka nilai d sekitar 2,5 % (0,025) atau lebih kecil lagi. Penyederhanaan Rumus diatas banyak dikenal dengan istilah Rumus Slovin.
Refensi :
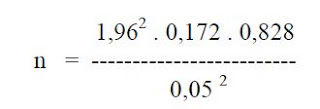


0 komentar :
Posting Komentar